1.伝送線路解析に必要な回路理論
シミュレーションの講座なのですが、なかなかシミュレータの具体的な話題にならずに、面食らっているかとも多いでしょう。何度か説明していますが、シュミレータを使う上で最も重要なことは、シュミレーション結果の判断です。
このために、最初に、シミュレーション結果の判断をするための、基礎的な電気回路の理論をおさらいします。
伝送線路回路の基本的理論は、特性インピーダンス、反射係数なのですが、その他にも、パルス回路と呼ばれる分野の理論も必要です。これは、方形波入力に対する波形の歪みの理論で、具体的には、微分回路や積分回路と呼ばれる理論です。これと共に、共振回路の知識も必要になります。
これは、今注目を集めているPI解析の基礎的な理論です。微分、積分回路や共振回路では、時定数とかQなどの知識も必要となってきます。
これらの理論の基礎について、これから数回にわたって説明します。
微分回路、積分回路、共振回路などは全てキャパシタ(容量)とインダクタ(誘導)とレジスタ(抵抗)の性質が基本になっています。
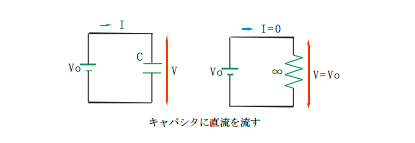
まず、直流電流を流すと、キャパシタはインピーダンスが無限大になり、電流を流しません。インダクタはインピーダンスが0で端子間には電圧が生じません。レジスタは一定の抵抗値を持ち、端子間にオームの法則に従った電圧を発生させます。
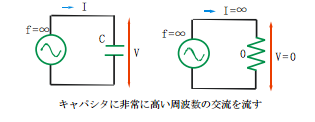
逆に、周波数が無限大に高い電流を流すと、インダクタはインピーダンスが無限大になり、電流を流しません。キャパシタはインピーダンスが0で端子間には電圧が生じません。
レジスタは周波数に関係なく一定の抵抗値を持ち、端子間にオームの法則に従った電圧を発生させます
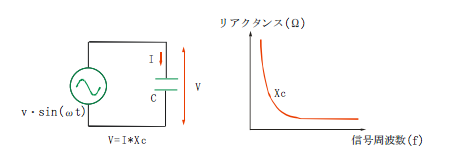
もう少しキャパシタとインダクタの性質を詳しく見ましょう。キャパシタに交流電圧を加えてみましょう。
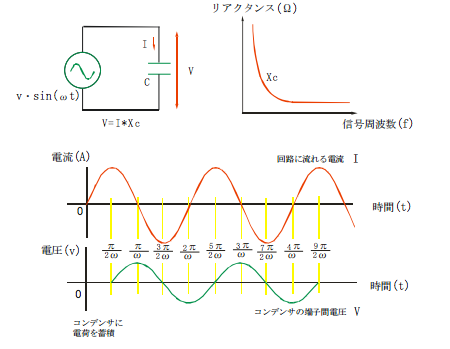
先ずキャパシタに加わる電圧が0から徐々に上昇した場合、キャパシタには電圧の上昇に従い、電荷が蓄えられます。この時、電流iは流れますが、キャパシタの端子間の電圧は、最初は0で、電荷が溜まるに従い、電圧が上がってきます。
次に、電圧が最高値から徐々に下がってきた時、キャパシタは蓄えていた電荷を放出して、電圧の変化を抑えるように働きます。しかし、キャパシタの電荷が少なくなるに従って、キャパシタの端子間電圧も下がってきます。
このように、キャパシタは、端子間の電圧変化を妨げようとします。このため、キャパシタの端子間電圧は、電流の変化よりも少し遅れて変化します。つまり、交流波形での、位相が違います。
キャパシタによる損失を容量リアクタンスXcと呼びます。
このリアクタンスはキャパシタの容量Cと、正弦波の周波数f(角速度ω)で決まります。
Xc=1/2πfC=1/ωC
キャパシタのリアクタンスに拠る電流と電圧の大きさの関係は
|V|=|I・Xc|
(電圧の位相はπ/2遅れる)が成立します。
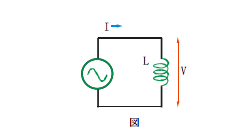
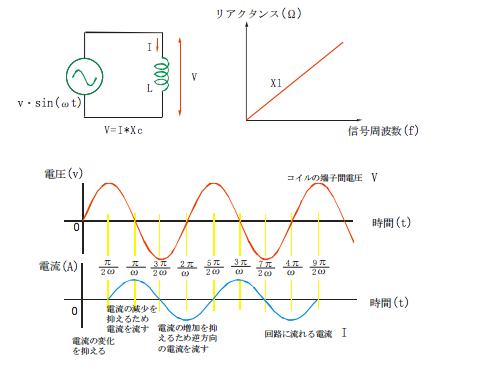
コイルに交流電圧を加えてみましょう。
コイルは、周波数が0だと、抵抗値が0で、電流を通すのですが、周波数が高くなれば、なるほど抵抗値が高くなって、どんどん電流を通しにくくなってきます。コイルに交流電圧を加えた時のコイルの動作をもう少し詳しく見てみます。
先ずコイルに加わる電圧が0から徐々に上昇した場合、コイルには自己誘電により、この電圧上昇によって流れる電流iと逆方向の電流が流れます。
このため、コイルの端子間の電圧はvですが、最初はコイルには電流が流れません。次に、電圧が最高値から徐々に下がってきた時、コイルは電流の減少に反対して電流を増大させます。
このように、コイルは、電圧の変化によって回路に流れる電流の変化を妨げる方向に電流を流します。正弦波では、電圧は周期的に変化しますから、コイルに流れる電流は常に電圧の変化によって流れる電流を妨げるように、電圧の変化に従って周期的に変化します。
このように、コイルに流れる電流は、電圧の変化よりも少し遅れて変化します。
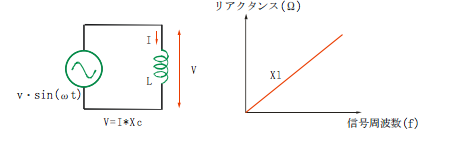
コイルによる損失を誘導リアクタンスXlと呼びます。
このリアクタンスはキャパシタの容量Cと、正弦波の周波数f(角速度ω)で決まります。
Xl=2πfL=ωL
コイルの誘導リアクタンスに拠る電流と電圧の大きさの関係は
|V|=|I・Xl|
(電流の位相はπ/2遅れる)が成立します。
ここまでは、正弦波で、キャパシタとインダクタの基本的な性質を考えてきました。
いよいよ、ディジタル回路で扱う方形波で素子の性質を考えましょう。方形波は、多くの周波数の正弦波が合成されたものですから、基本は、正弦波に対する応答と同じです。
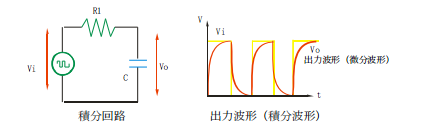
方形波をCに接続した回路に入力します。
この場合は、負荷がCの回路です。直流の時には、キャパシタのリアクタンスは無限大ですから出力は入力と同じになります。ある周波数に正弦派に対しては、リアクタンスは決まった値になりますから、出力は、抵抗の値と、リアクタンスの値で、入力を分割した少し低い電圧が現れます。
周波数が高くなると、キャパシタのリアクタンスはどんどん小さくなりますから、出力電圧は下がってきます。
方形波を入力にしますと、方形波は、色々な周波数の正弦波の合成されたものですから、周波数の低い成分は電圧が高く、周波数の高い成分は電圧が低くなります。方形波の場合は、立ち上がり、立ち下がりのときの鋭い変化は、大変に周波数が高いので、この高い周波数に対するキャパシタのリアクタンスは低く、電圧は低くなります。
このため、方形波入力に対しては、立ち上がりがゆっくりになったなだらかな波形が出力されます。この波形のことを積分波形と言い、このように、入力パルスをなだらかにする回路を積分回路と呼びます。
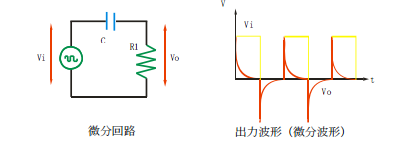
逆にRとCを接続した回路で、抵抗両端の電圧をみると、リアクタンスの値の周波数の変化が逆に働き、図のような波形になります。このように高い周波数の成分の損失が小さく、低い周波数成分の振幅が小さくなるような波形を微分波形と呼び、このように高い周波数を残し、低い周波数成分をカットする回路を微分波形と呼びます。
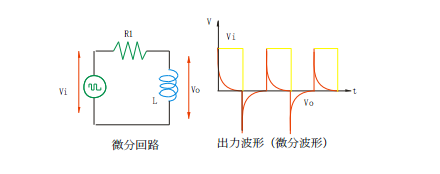
次に、抵抗とコイルを直列に接続した回路のコイルの両端の電圧について考えましょう。この場合は、負荷がLの回路です。直流の時には、コイルのリアクタンスXlは
Xl=2πfL
で、f=0ですから、ゼロで、コイルの両端の電圧はゼロです。 正弦派を入力すると、低い周波数では、リアクタンスの値は小さいのですが、周波数fが高くなりますと、コイルのリアクタンスはどんどん大きくなります。このため、コイルの両端の出力電圧は上がってきます。
入力波形が方形波の場合、方形波は、多くの周波数の正弦波の合成されたものです。コイルの端子には、周波数の低い成分は小さく、周波数の高い成分は大きな電圧が表れます。これは方形波の部分波形で、この回路は微分回路です。
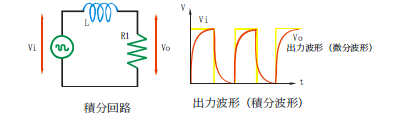
同様に、図1の回路で、方形波を入力した時の抵抗Rの端子間電圧を見ると、コイルのリアクタンスが大きくなると、回路に流れる電流が小さくなるので、抵抗Rの端子間電圧は小さくなります。
V=I・R
つまり、周波数の低い成分の電圧は大きく、高い成分の電圧が小さい、積分波形になります。
パルス・ディジタル回路では、正弦波の位相ではなく、正弦波の周波数の違いによる回路の特性の違いが重要です。この、微分回路と積分回路はパルス・ディジタル回路の基礎で、この回路の考え方が、ノイズ発生のメカニズムの理解やノイズ対策に役立ちます。